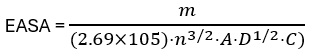Calculating the Electroactive Surface Area
And Challenges To Watch Out For
Calculating the Electroactive Surface Area of your Electrodes
Electrochemists often work at the intersection of theory and application, transforming abstract principles into practical solutions. One crucial parameter, particularly in the context of biosensors, batteries, and catalysts, is the electroactive surface area (EASA). While it may seem like a straightforward calculation, understanding its nuances can have a significant impact on the performance and interpretation of electrochemical systems.
So, why does EASA matter?
The EASA represents the actual electrode area available for electrochemical reactions, which is distinct from the geometric area—the physical size of the electrode. This distinction is critical because the EASA directly affects key performance metrics. For example, current density is normalised to the EASA to provide a clearer picture of reaction efficiency. In biosensors, a larger EASA enhances sensitivity by providing more interaction sites for analyte detection. In catalytic systems, understanding the EASA is key to evaluating and comparing materials effectively.
How can you determine the EASA?
Several electrochemical techniques are commonly used, depending on the system and the tools available. Below I will describe three methods for calculating the EASE and outline some common challenges to be aware of.
The first method we will discuss utilises cyclic voltammetry (CV). By performing CV in the presence of a well-characterised, reversible redox system like ferri/ferrocyanide ([Fe(CN)6]3−/4− ) the peak current (Ip) is directly related to the EASA through the Randles-Sevcik equation:
Where:
Ip = Peak Current (in Amps)
n = Number of electrons transferred (n=1, for [Fe(CN)6]3−/4− redox system)
A = Electroactive surface area (in cm2)
D = Diffusion coefficient for the redox probe (D = 6.5 x 10-6 cm2/s for 2 mM [Fe(CN)6]3−/4− in 0.1 M KCl)
C = The concentration of the redox species (mol/cm3)
v = Scan rate (V/s)
By carrying out CV at different scan rates (v) and plotting the corresponding peak current (Ip) against ν1/2, the slope of the resulting linear graph can be used to determine the EASA: